Primary teachers, understanding common misconceptions in fractions and how to fix them can really help your students.
Many students think fractions are tough, especially when solving word problems involving fractions.
It becomes even more challenging when they start believing things that aren’t true.
Remember, it’s better to prevent mistakes than to fix them later.
Once we know about these fraction mistakes, we can help our students avoid them.
This article will explore three common mistakes and how to correct them.
1) Misconception 1: Don’t regroup when subtracting of Mixed Numbers.
When students see that the numerator of the subtrahend is bigger than the numerator of the minuend, they are stumped.
One common error is they will just take the bigger number to subtract the smaller number.
Solution 1
To work about the whole regrouping process, students can just change the mixed numbers into improper fractions to work on it.
The cons about this method are that sometimes the number can get real big and students may make careless mistakes when they convert or calculate. (This also means they didn’t learn the method of regrouping.)
Solution 2
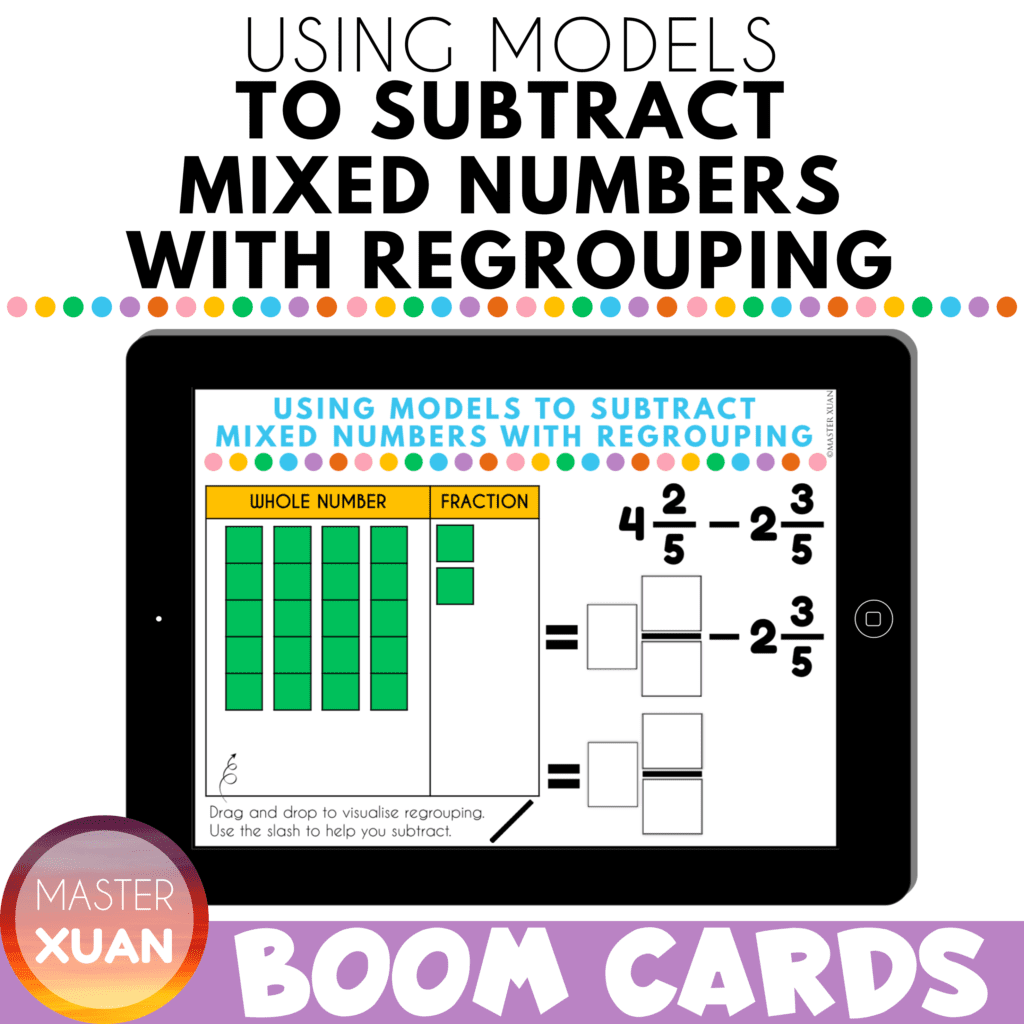
Use visual aids or manipulatives to show what regrouping of fractions really means.
Many students didn’t know that the number of parts in 1 whole is the denominator. Remind them about it!
If you need more practice, get these self-checking digital task cards that allow students to shift the online manipulatives to help them solve the questions.
Subtraction of Mixed Numbers with Regrouping
2) Misconception 2: Ignoring the units of fractions.
This is a really serious and common misconception that I saw many students have in Singapore.
I mentioned it in the previous blog post – 5 Popular Primary 5 Fraction Word Problems You Need To know.
I’ll change the question a bit to make my point.
Question:
Bryan has 40 kg of flour. He uses ⅕ of it to bake some cakes. Then, he uses ¼ kg of flour to bake some cookies. How much flour does Bryan have in the end?
There are 2 possible wrong ways students will make as they ignore the units and treat ¼ kg as the same way as ⅕.
1st wrong solution: 40 – ⅕ – ¼
2nd wrong solution:
⅕ + ¼ = 9/20
9/20 x 40 = 18
40 – 18 = 22
I once asked my student why he multiplied ¼ with 40 kg. His response was because of the keyword “of”.
Previously when they first learned multiplication of fractions, they learned the language this way: ¼ of 40 is ¼ x 40 = 10. They learned that “of” can stand for multiplication.
Solution 1
One possible way is to reteach and let them know that ¼ kg stands for ¼ of a kg and that value refers to the weight of the flour.
Solution 2
Another way is to point out to them that fraction with units refers to value. Only a stand alone fraction is a fraction, or a part of a value. I like to indicate on the question that the fraction is a V, value, or a F, fraction, to make it clear to them.
3) Misconception 3: Always making fractions of different items the same denominator.
This misconception is closely related to the previous one, where students overlook the units, assuming they both represent the same whole. This leads them to mistakenly make the denominators the same.
Students often practice making the denominators of unlike fractions identical, making it almost second nature to do so upon encountering them.
However, they tend to forget that aligning the denominators is only necessary when the fractions refer to the same whole or quantity.
Thus, they got it wrong for doing so for fraction word problems such as equal to or remainder concept.
Solution
I remind students how crucial it is to know what makes up the whole. I’ll give them an example: a fraction of $1 and a fraction of $1 million is so big of a difference.
Then, I’ll draw models to visualize what the fractions really mean.
Disclaimer: The solution might not always work. Sometimes, you have to allow your students to make mistakes in order to learn.
Here’s a metaphorical story for how I felt when I first learned and taught about common misconceptions in fractions.
Imagine finding a hole in the ground and warning my students not to fall into it.
However, despite my caution, they still end up doing just that.
Urgh! (Make me want to bang my head.)
Then I think, maybe they forgot about it because it was taught like 10 minutes ago. So I try to place warning signs around aka write it on the board and keep it there while they do the question.
But, as expected, they still fall into it.
Lesson learned: Instead of warning them beforehand, let them fall and laugh in their face afterwards (just kidding…or not).
Final Thoughts
There are numerous misconceptions in fractions stemming from a lack of conceptual understanding during the learning process.
Additionally, students often make common errors when performing the four operations of fractions. However, these errors are relatively easier to correct, in my opinion.
This article, however, focuses on other misconceptions in fractions that are constantly made by students even after teaching them for months.
If you’re curious about common errors in fractions, feel free to DM me on Instagram (@learningwithmasterxuan)!
Lastly, remember that it is completely normal for students to make the same mistakes over and over again. Just take a deep breath and teach them like you just taught them the very first time (of course, change your strategies if needed)!
Here are some additional resources if you need more practice on Word Problems On Fractions!

Here are some pins that you can save to bookmark this post. Save them to your Pinterest Board now! ↓







