If you want to master ratio in word problems in Singapore primary math placement test, you need to know these 7 concepts.
Of course, there are many other types of questions involving ratio, but these questions types that I’m sharing in this blog post are those that are commonly tested in school.
Here are the 7 basic concepts:
- Using ratio as units
- Repeated Identity
- Part-Whole Relationship
- Total Unchanged
- Difference Unchanged
- Quantity Unchanged
- Units & Parts
In this blog post, I will be going through how to identify the concept, give examples of ratio word problems, and show you how to answer ratio word problems.
You can find similar questions in Word Problems On Ratio and Ratio Activity For 6th Grade, available in my TpT store.

1) Using ratio as units
This is not an actual concept but more of a question type. This usually appears when the teacher introduces ratio to students in Primary 5.
Basically, you can use the ratio as units to solve the question.
Here’s one example:
Mary, Nancy and Olivia shared 350 stickers in the ratio 3 : 2 : 5. How many stickers did Mary and Olivia have altogether?
(Maris Stella Primary School 2021 Prelim Paper 1 Q10)
3 units + 2 units + 5 units = 10 units
10 units = 350
1 unit = 350 ÷ 10 = 35
Mary + Olivia = 3 units + 5 units = 8 units
8 units = 35 x 8 = 280
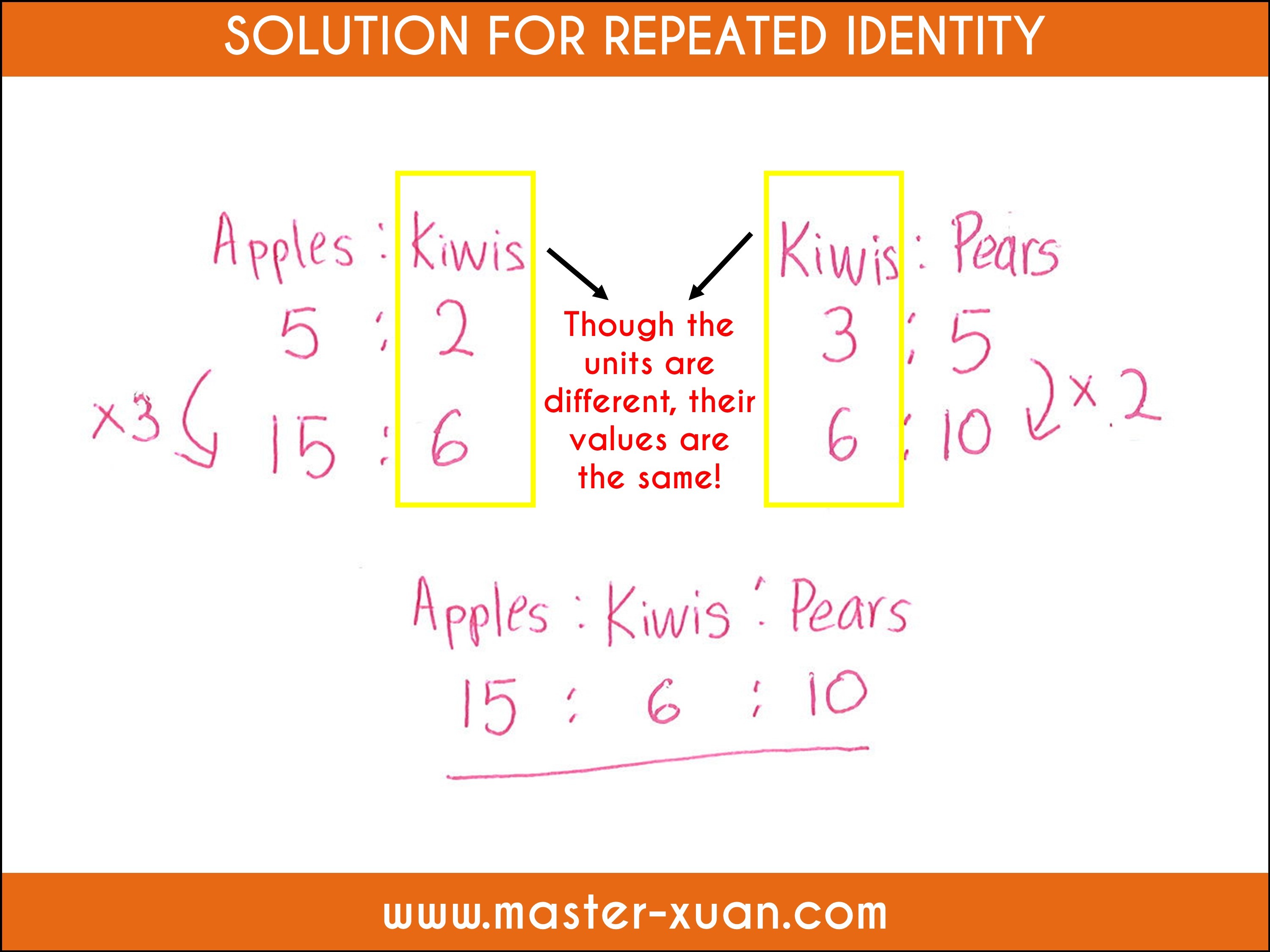
2) Repeated Identity
What is repeated identity?
When 1 variable, object, or individual is being compared twice, it is a repeated identity. Usually, the units will be different but do take note that their value is the same. Hence, to solve repeated identity, we need to make the units of the repeated identity equivalent.
Usually, in a ratio word problem, the question will state 2 ratios and there will be 1 individual that is being compared in both ratios.
In a basket, there are some apples, kiwis and pears. The ratio of the number of apples to the number of kiwis is 5 : 2 while the number of kiwis to the number of pears is 3 : 5. Find the ratio of the number of apples to the number of kiwis to the number of pears.
(St. Gabriel Primary School 2021 SA1 Paper 2 Q2)
3) Part-Whole Relationship
Usually, I label this for questions that provide a ratio of a sub-group that is part of a bigger group.
For example:
The pupils at a camp are divided into Group A and Group B. The ratio of the number of boys to girls in Group A is 5 : 4. The ratio of the number of boys to girls in Group B is 5 : 1. There are 3 times as many pupils in Group B as in Group A.
Which of the following could be the total number of boys in both groups?
- 17
- 30
- 40
- 55
(2020 PSLE Paper 1 Q15)

4) Total Unchanged / Constant Total
Total Unchanged is under the broad category of before and after ratio word problems.
Total unchanged is identified by:
- Before ratio
- Change: Internal transfer (Subject A will give Subject B)
- After ratio
Since the total value before and after the changes didn’t change, make the total units of both ratios be the same. Only when the total units are the same, the value of the units before and after will be the same.
This concept can also apply when the total number of individuals in both groups/ratios are the same.
An equal number of children attended Camp A and Camp B. The ratio of the number of girls to the number of boys in Camp A was 5 : 9. The ratio of the number of girls to the number of boys in Camp B was 4 : 1. Altogether, there were 132 more girls than boys. How many children were there in both camps?
(Rosyth Primary School 2021 Prelim Paper 2 Q11)

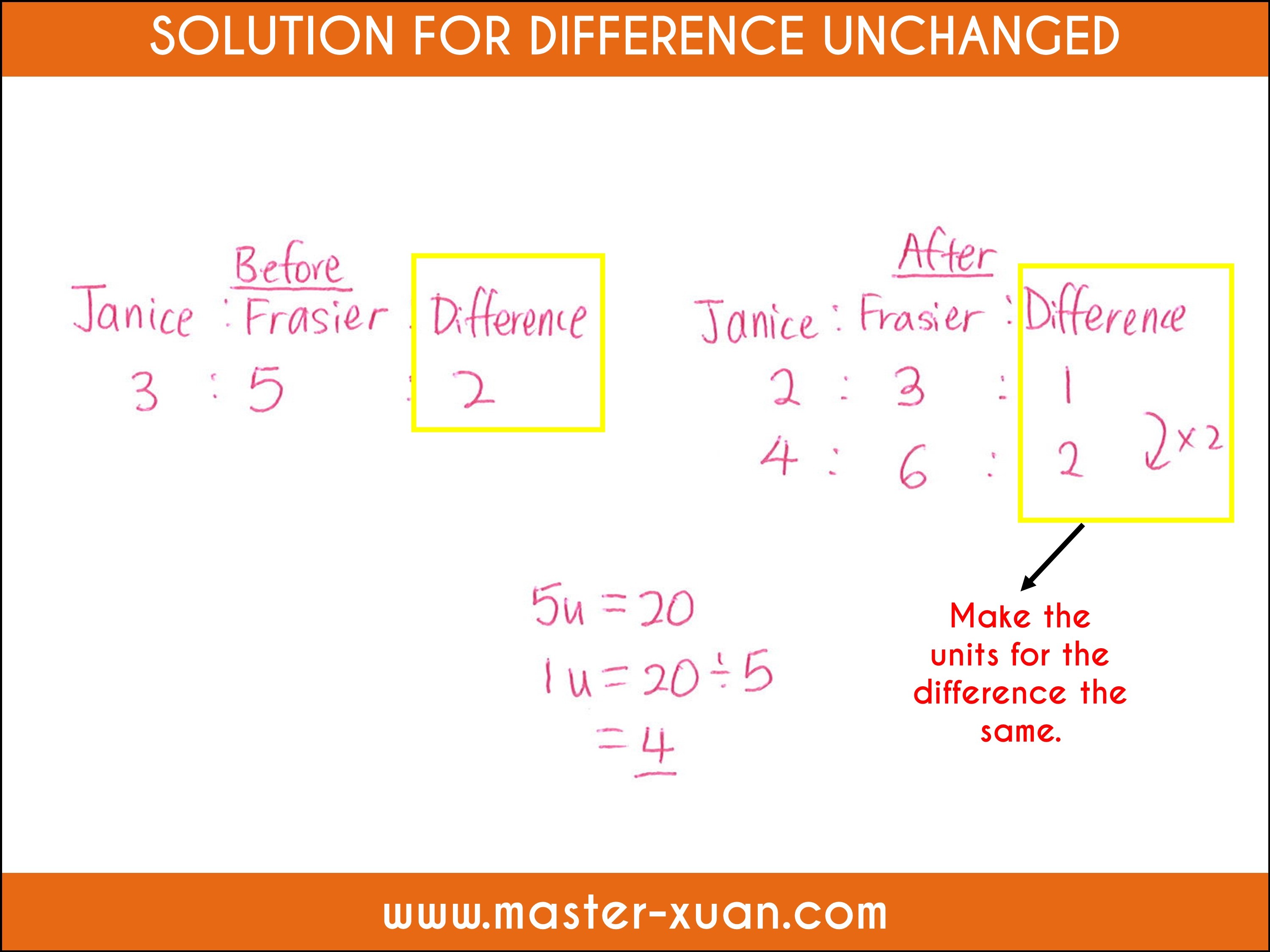
5) Difference Unchanged / Constant Difference
Difference Unchanged is under the broad category of before and after ratio word problems.
Difference unchanged is identified by:
- Before ratio
- Change: Equal amount removed or added to both individuals
- After ratio
Usually, age questions involving ratio will be difference unchanged as the characters will grow at the same rate.
The ratio of Janice’s age to Frasier’s age is 3 : 5. Frasier is 20 years old now. In how many years’ time will the ratio of Janice’s age to Frasier’s age be 2 : 3?
(Holy Innocent Primary School 2018 Prelim Paper 2 Q2)
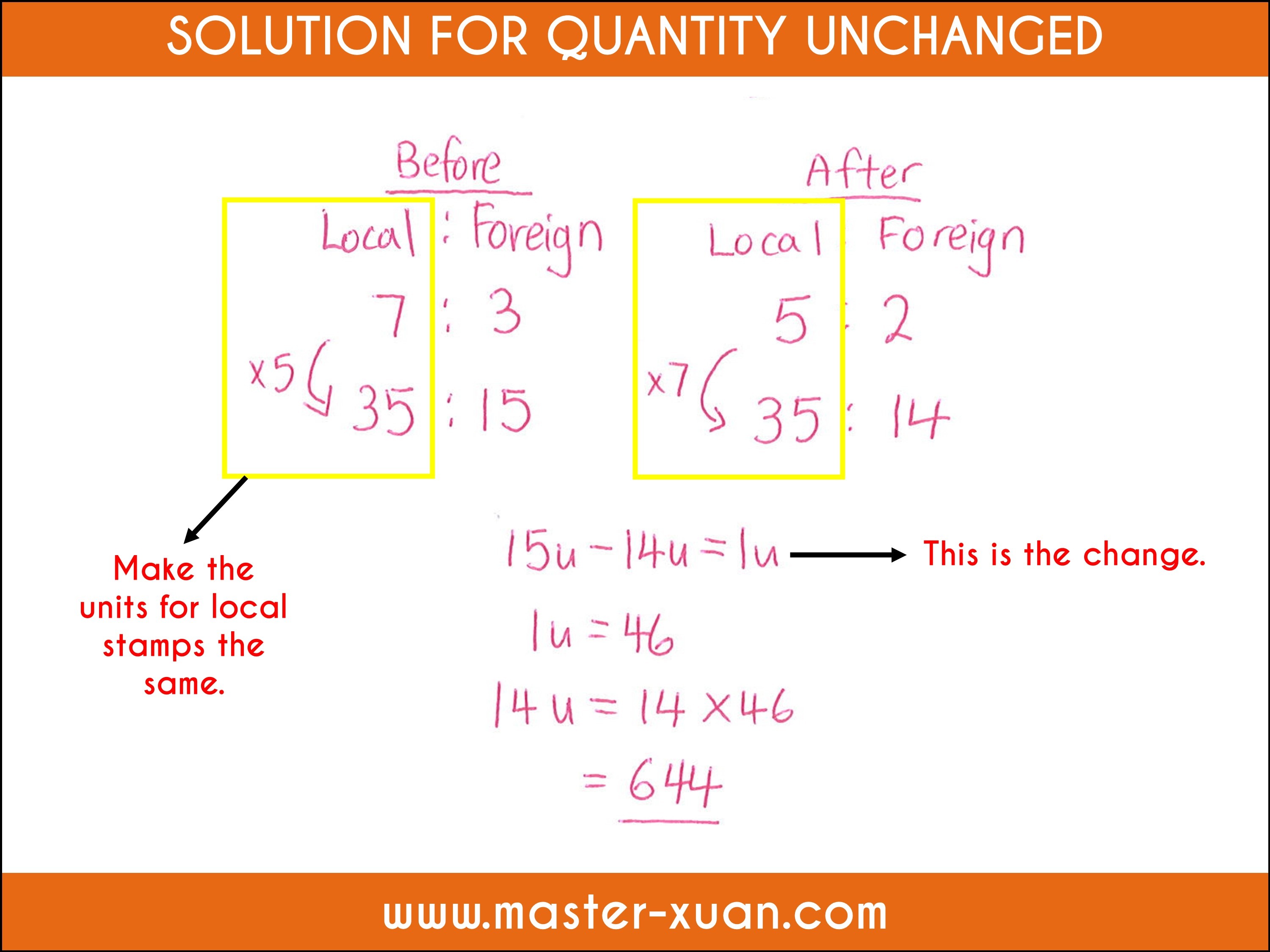
6) Quantity Unchanged / Constant Quantity
Quantity Unchanged is under the broad category of before and after ratio word problems.
Quantity unchanged is identified by:
- Before ratio
- Change: Only 1 individual add or remove values
- After ratio
This is similar to repeated identity, the difference is this concept involves changes (external transfer).
John had a collection of local and foreign stamps. The ratio of the number of local stamps to the number of foreign stamps he had at first was 7 : 3. After giving away 46 foreign stamps, the ratio of the number of local stamps to the number of foreign stamps became 5 : 2. How many foreign stamps did John have in the end?
(Raffles Girls’ School 2019 Prelim Paper 2 Q1)
7) Units & Parts
Units & Parts is under the broad category of before and after ratio word problems.
Units & parts concept is identified by:
- Before ratio
- Change: Everything changes such as external transfer for both individuals
- After ratio
The ratio of the number of Jayden’s pens to the number of Mike’s pens is 3 : 5 at first. After Jayden bought another 6 pens and Mike bought another 5 pens, the ratio of the number of Jayden’s pens to the number of Mike’s pens became 3 : 4. How many pens did Mike have in the end?
(Maris Stella Primary School SA1 2021 Paper 2 Q15)
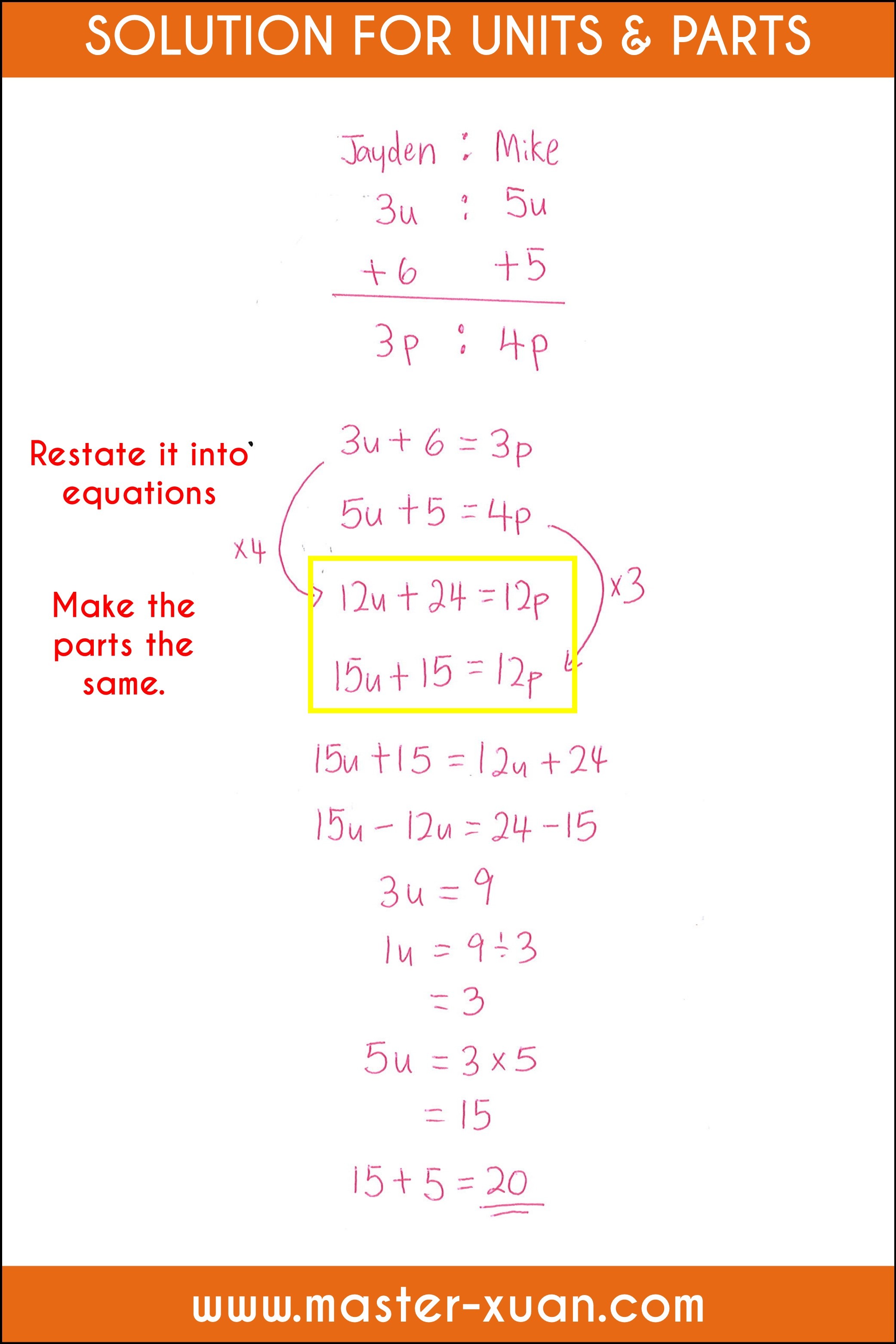
Conclusion
To recap, here are the 7 ratio question types:
- Using ratio as units
- Repeated Identity
- Part-Whole Relationship
- Total Unchanged
- Difference Unchanged
- Quantity Unchanged
- Units & Parts
If you want to solve more ratio word problems that could appear in PSLE in Singapore buy Word Problems On Ratio to practice it seriously and/or buy Ratio Activity For 6th Grade to have fun reviewing them.

Here are some pins that you can save to bookmark this post. Save them to your Pinterest Board now! ↓







